I've already used it in the previos post, but not mentioned it: HERE you find a great way to post LaTeX in your blog. It's very simple, just enter the formulas and copy the html-code into your blog.
The editor itself is great. It is fast and got many features like shortcuts to important commands and auto-closing brackets. Also, the result itself (the image) as well as the html-code is presented just in time!
Another important thing: it's open-source, so you can use it without any limitations (at least I haven't read something different yet).
Sunday, February 6, 2011
Saturday, February 5, 2011
You think there are many rational numbers? You're wrong.
I want to share something very interesting with you that told me my calculus teacher the other day.
Take the rational numbers in the closed interval from 0 to 1. It's easy to see, that this set is given by
So the numbers in this set are countable. Let's call them
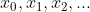
Now let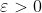
. Cover every 
with an interval of length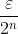 
, that is
It follows that the measure of the union of the Intervals fulfills:
 \leq \sum_{n=0}^{\infty}\frac{\varepsilon}{2^n} = \frac{\varepsilon}{1-\frac{1}{2}} = 2\varepsilon "\mu\left ( \bigcup_{n=0}^{\infty} I_n \right ) \leq \sum_{n=0}^{\infty}\frac{\varepsilon}{2^n} = \frac{\varepsilon}{1-\frac{1}{2}} = 2\varepsilon")
So what we see is: if we chose the epsilon small enough, the rational numbers, including the intervals around them, cover nearly no space in the interval from 0 to 1! That means, the space is coverd almost entirely by the irrational numbers.
I think this fact shows us very well what the difference between "countable" and "uncountable" sets is, and how much more irrational numbers than rational numbers there are even though they are both infinite many.
Have fun thinking about this!
Take the rational numbers in the closed interval from 0 to 1. It's easy to see, that this set is given by
So the numbers in this set are countable. Let's call them
Now let
It follows that the measure of the union of the Intervals fulfills:
So what we see is: if we chose the epsilon small enough, the rational numbers, including the intervals around them, cover nearly no space in the interval from 0 to 1! That means, the space is coverd almost entirely by the irrational numbers.
I think this fact shows us very well what the difference between "countable" and "uncountable" sets is, and how much more irrational numbers than rational numbers there are even though they are both infinite many.
Have fun thinking about this!
Welcome to my new blog!
I'll write about many different things: Much about maths and physics (because that's what I'm studying), but also about other things I like to talk about. Like art and music, politics and society, traveling, ...
I hope you enjoy browsing my blog and I'm looking forward to reading your comments!
- Michael
I hope you enjoy browsing my blog and I'm looking forward to reading your comments!
- Michael
Subscribe to:
Posts (Atom)